1. Introduction
Selective or differential blasting is a recently developed technological lever proposed by the Cooperative Research Centre for Optimising Resource Extraction, known as CRCORE, to efficiently separate ore from waste in Grade Engineering® (Carrasco et al., 2016; La Rosa, 2017). The main goal of differential blasting is to blast the ore finely and the waste coarsely. Therefore, differential blasting is a combination of ‘mine to mill’ (M2M) (McKee, 2013; Scott et al., 2009; Scott et al., 2002) blasting, to maximise the ore fines with a limited top size, and the ‘less fines’ (LF) approaches to quarrying (Moser, 2005, Moser, 2006) which are used to maximise diggable waste fragments above a threshold sieve size. Then, early removal of waste by sieving and sorting reduces unnecessary energy and time-consuming mechanical comminution (Walters, 2017). For optimal outcomes, the design of the hole spacing and explosives distribution must be varied in three-dimensions to match the spatial variations of the grade, and geotechnical, geological, and geo-metallurgical distribution in the rock mass (Sellers et al., 2019; Usami et al., 2019).
The experience of the authors has been that the proper characterisation of rock masses before blasting is often difficult due to production and data constraints. Data to characterise the rock mass is scarce. This review arose from a search for the key geological and geotechnical parameters that can be identified in a fast and continuous manner for differential blasting in large open-pit mines. The outcomes of this review paper may help to produce updated definitions of the rock mass blastability, to identify the parameters that have the first-order effects in the assessment of the blastability of rock masses, and determine those that can be modified to easily develop the three-dimensional (3D) distribution of blastability.
The main aim of blast design is to use explosive energy to break rock masses into sizes and shapes that can facilitate subsequent operations (e.g., excavation, loading, hauling, crushing, and milling). Correct fragmentation reduces the overall costs and time of the extraction and comminution of ores in both surface and underground mining operations (Ouchterlony, 2003; Sanchidrián and Ouchterlony, 2017a). Blasting has also conventionally been used to excavate civil structures in hard rocks, e.g., for road trenches, tunnels, and underground caverns (Jimeno et al., 1995; Ouchterlony et al., 2002). Undesirable technical and environmental issues such as excessive back-break and over-break, overpressure, flyrock, and ground vibration arise from poor blast designs or conflicting requirements, such as high intensity blasting near a pit wall (Müller, 1997; Müller et al., 2010a; Segarra et al., 2010).
The process of rock fragmentation during blasting is complex and involves several stages in the loading and deformation of rocks (Jimeno et al., 1995; Nielsen and Malvik, 1999). Around 20 % to 40 % of the blast energy is normally consumed by the pulverizing and heavily crushing of the rocks surrounding the blast hole (Hamdi et al., 2001; Jimeno et al., 1995; Ouchterlony et al., 2004; Sanchidrian et al., 2007; Sanchidrián et al., 2018). Analytical models (Cunningham et al., 2007) and numerical simulations (Onederra et al., 2009; Sellers et al., 2012a) have shown that crushing depends on the non-elastic distortion characteristics of the rock during the blasthole expansion. As the explosive expands the blasthole further, cracks appear within the rock and are driven by the local stresses. Further from the blasthole, and in areas of limited exposure to increased stress after detonation, the rock separates on weaker discontinuities present in the rock mass, so the rock is liberated not fractured (Chertkov, 1985, Chertkov, 1986).
The design of the blast and the numerous in-situ characteristics of the rocks govern the mechanisms of the breakage and control the fragmentation (Bohloli et al., 2001; Hamdi et al., 2007; Ouchterlony, 2003). Multiple terms like blastability, crushability, breakability, fracturability, explodability, explosibility, and fragmentability are used to refer to the geological and geotechnical characteristics of a rock mass influencing blast outcomes (Da Gama, 1995; Jimeno et al., 1995; Kutuzov et al., 1974; Michik and Dolgov, 1966; Rustan et al., 1983; Shapiro, 1988). The rock mass blastability has historically been defined as a factor that shows the resistance of rocks to blast loads. There are, however, blastability assessment approaches that involve the blast design parameters, such as the characteristics of the explosive charges or the measurement of the outcomes. There is, therefore, no widely accepted technique available to assess the blastability of rock masses and many efforts at unification have been attempted (Dey and Sen, 2003; Scott, 1996; Widzyk-Capehart and Lilly, 2002).
The definition of the rock mass blastability proposed by Ouchterlony (2003) can help to improve the conventional abstract definition of rock mass blastability and to eliminate the uncertainties associated with identifying the parameters that should be considered. According to Ouchterlony (2003), blastability is applied to link the effects of the geological and geotechnical parameters of a rock or rock mass to the outcomes of fragmentation prediction. For example, the average fragment size, x50, is defined as:
Here, the rock factor represents the blastability of the rock mass. A general form of Eq. 1, has also recently been proposed by (Ouchterlony et al., 2017) and (Sanchidrián and Ouchterlony, 2017a) which can be used to estimate the size of particles associated with each percentage passing (p) and may be written as:
This means that the rock mass blastability quantifies the compound effect of the geological and geotechnical site factors on fragmentation, either as a single representative value or as a whole size distribution. The role of the blast designer is to change the geometry and explosives factors to obtain their desired fragmentation outcome, given the rock factor of the blast block.
The future of blasting will include automated loading systems (Lilly, 2011; Lovitt and Wicks, 2017; Sellers et al., 2012b) and the ability to change the explosive density and energy along the hole (Halander et al., 2015). Therefore, blast designs should now incorporate three-dimensional (3D) distribution of the blastability of the rock mass even though estimating the spatial distribution might be very challenging in practice (Rustan et al., 1983). From Eq. 1, if the blast geometry and explosives factors can change across the blast block, this means that there is a need to identify how the blastability varies in 3D space.
In the present paper, the factors controlling the design of blasts are discussed first to identify the components and how the blastability assessments are used: qualitatively, to determine the powder factor and for fragmentation prediction models. The inputs into the blastability assessments are then categorised based on the source of the parameters, starting with laboratory tests (Section 3.1), average rock mass measurements (Section 3.2), geotechnical ratings (Section 3.3), indirect pre- blast (Section 3.4), and post-blast (Section 3.5) measurements, to more complex methods based on large quantities of rock mass and blast data (Section 3.6). The commonalities between the parameters are discussed in Section 4.1 and the methods are compared in Section 4.2. The incorporation of geological variability is covered in Section 4.3. Finally, in Sections 4.4, the options for the application of automated geological logging, geostatistics, and geophysics to determine a 3D blastability assessment across a mining block and orebody are considered. A simple comparison of the blastability assessment approaches for application to develop a three-dimensional blastability distribution is also provided in the Appendix.
2. Overview of the application of rock mass blastability
This section presents an overview to identify consistent trends in the selection of the important input and output parameters in blast design, and how these are related to the assessment of blastability.
2.1. Factors controlling blast outcomes
The efficiency of a blasting operation is highly dependent on the mechanical parameters of the rock mass that govern the responses to blast waves, the geometrical parameters of the blast design that affect the distribution of the blast energy in space (e.g., borehole bottom and column energy) and the time factors (e.g., delays between holes/rows) that control the release and transmission of explosive energy to the surrounding rock mass, in time and during the blasting (Hamdi and du Mouza, 2000, Hamdi and du Mouza, 2005b). Similarly, Latham et al. (2006) grouped the effective factors in rock blasting as follows:
A – Factors that are dictated by the geological and geotechnical characteristics of the blasting site:
-
-
The mechanical and geometrical characteristics of discontinuities (e.g., bedding, schistosity and foliation, faults). The spacing of discontinuities, orientation, and the cohesion of joints are typical examples of such parameters.
-
-
The strength and deformational properties of rocks (e.g., rock type, weathering status).
-
-
The density, porosity, and permeability of rocks.
-
-
The presence of water in blast holes or discontinuities.
-
-
The spatial variations of the geology and rock types.
B – Factors that are associated with the blast design (this category does not depend on the inherent features and characteristics of the blasting site):
-
-
Blast design parameters (e.g., configuration and drilling pattern).
-
-
Properties and detonation methods of charges and the application of timings to control the distribution of energy into the rock mass.
Therefore, according to Latham et al. (2006), any blastability assessment approach shall quantify the effects of the geological and geotechnical characteristics of rocks in the blast block (first category) so that the blast design factors (second category) can be adjusted to achieve the desired output, based on the purpose of the blast. This is consistent with the definition of the blastability proposed by Ouchterlony (2003) (see the Introduction).
2.2. The applications of the assessments of blastability
The outcomes of the blastability assessment approaches can help to identify consistent trends in the selection of the governing geological and geotechnical parameters in different blast designs. Such detailed information can be used to design advanced differential or selective blasts to optimise the fragmentation of the rock based on the requirements of the downstream processes (e.g., loading, mechanical crushing, milling), to improve the efficiency of the fragmentation and to reduce the undesirable consequences of the blasting (e.g., ground vibration, overbreak, underbreak, back break, and fly rock).
Müller (1997), and Müller and Hohlfeld (1997) showed that characterising the rock masses for blasting and finding the matched explosive and blast design not only helps to improve the fragmentation but can reduce the undesired consequences such as ground vibration, flyrock, and back break. Similarly, Ashby (1981) performed several field test blasts in a copper and gold mine and stated that to reduce the blast-induced damage the first step is to improve the fragmentation by applying proper rock mass characteristics, in the production zones. These show that different objectives of the blast may not be independent. The blastability can, therefore, be considered as a rock or rock mass property, which is linked to the fragmentation. The blastability provides unique fragmentation results for each blast set up and does not depend on the purpose of blasting. Fitting the fragmentation to that purpose of blast design is, however, the role of the blast design parameters, which was previously discussed in the second category of effective factors by Latham et al. (2006) (see Section 2.1).
From the historical thread of the literature, three principal approaches to the application of the assessment of blastability in blast design have been identified and are discussed here: the qualitative assessment, the prediction based on powder factor (mass of explosive per unit volume of rock), and the direct prediction of fragmentation distribution.
2.2.1. Qualitative assessment
An early blastability classification was proposed by Aleksandrov et al. (1963) which was presented in Mosinets et al. (1967). This qualitative assessment scheme was developed based on field inspections and qualitative assessments of several blasting outcomes at the Kal'makyr mine, in the former Soviet Union. Kal'makyr mine is located in the east of Uzbekistan, in Tashkent Province, and is among the largest copper reserves in the world. The blasts, considered in the development of this classification, aimed at obtaining good rock breaking to achieve continuous operation. Aleksandrov’s blastability classification is also known as the Central Research Institute’s (CRI) classification. According to the CRI classification, rock masses may be classified into:
Category I: Easily blasted: small blocks, strongly fractured, with average discontinuity spacing around 0.15 m. This can be interpreted as providing a finer fragmentation for a given specific charge or requiring a smaller specific charge to obtain the desired fragmentation.
Category II: Medium ease of blasting: medium size blocks with average discontinuity spacing around 0.5 m. This may also be interpreted as providing a medium fragmentation for a given specific charge or requiring a medium-specific charge to obtain the desired fragmentation.
Category III: Difficult blasting: Large blocks of rocks with average discontinuity spacing over 0.5 m. This can also be considered as resulting in a coarse fragmentation for a given specific charge or requiring a considerably large specific charge to obtain the desired fragmentation.
However, this qualitative classification suffers from a few drawbacks, e.g., soft sedimentary rocks, like potash without discontinuities or hard jointed igneous rocks may result in different fragmentation when identical blast set up is used. The behaviour of rocks in blasting may not simply be classified based on the spacing of discontinuities. The classification approach is also subjective to personal judgment and the interpretation of the distance between discontinuities in a rock mass. The joint network can form blocks with different sizes with a specific particle size distribution, (PSD), which is also known as the in-situ block size distribution (IBSD). Additionally, this approach is only applicable to areas where rock discontinues are visible. Differentiation between the blast-induced cracks, caused by the firing of the previous rounds of blasting, and the natural discontinuities may also not be straightforward. In other words, the pre-conditioning of the rock mass by the previous blast rounds should be identified and considered.
2.2.2. Quantification using powder factor and energy
Sukhanov (1947) proposed using the powder factor, q (kg/m3), as a qualitative characterisation of the blastability of a rock mass for fragmentation design and developed a series of standard test conditions for this purpose (Sukhanov, 1947; Sukhanov and Kutuzov, 1967). Rocks were divided into sixteen classes according to the powder factor, that is needed to achieve the desired fragmentation, and a few other blast design factors. If the powder factor is high, the rock is more difficult to fragment, otherwise it is easy to blast. A series of correction factors were proposed to adjust the powder factor for non-standard conditions; however, these have proved cumbersome to use in practice. The classification also involves considerable levels of personal interpretation. Gokhale (2010) also reported on the work performed by researchers in the Soviet Union, e.g., Kutuzov (1979), to improve these qualitative categorisation schemes by including factors like the intact rock strength, rock density, and average joint spacing, Sj-av in (m). Typical examples of the powder factors needed to fragment the rocks for different rock types have been tabulated in
Table 1. It is also noted that in this table we summarised the classification based on Protodyakonov’s rock strength index for a rough comparison between the two different classifications schemes (see Section 3.1.1).
Table 1. Protodyakonov’s rock hardness index and Sukhanov's blastability classification schemes (adopted from Zou, 2017).
| Protodyakonov's classification | Sukhanov's classification | Typical rocks | ||||
|---|---|---|---|---|---|---|
| Class | Hardness description | fp | Blastability | Class | Powder factor (kg/m3) | |
| I | Extremely sturdy | 20 | Most difficult to blast | 1 | 8.3 | Dense micro-crystalline quartzite |
| 2 | 6.7 | Extremely durable quartzite | ||||
| 3 | 5.3 | Very dense quartzite and basalt | ||||
| II | Very sturdy | 18 | Very difficult to blast | 4 | 4.2 | Fine-grained andesite and diabase |
| 15 | 5 | 3.8 | Porphyritic quartz | |||
| 12 | 6 | 3.0 | Very fine-grained siliceous sandstone | |||
| III | Sturdy | 10 | Difficult to blast | 7 | 2.4 | Dense granite, and hard iron ore |
| IIIa | 8 | 8 | 2.0 | Tough and strong sandstone and limestone | ||
| IV | Relatively sturdy | 6 | Relatively difficult to blast | 9 | 1.5 | Sandstone |
| IVa | 5 | 10 | 1.25 | Sandy shale | ||
| V | Moderately sturdy | 4 | Moderate resistance to blast | 11 | 1.0 | Not very rough sandstone and limestone |
| Va | 3 | 12 | 0.8 | Competent and dense shales | ||
| VI | Fairly weak | 2 | Fairly easy to blast | 13 | 0.6 | Soft shale |
| VIa | 1.5 | 14 | 0.5 | Anthracite | ||
| VII | Weak | 1.0 | Easy to blast | 15 | 0.4 | Dense clay and soft coal rocks |
| VIIa | 0.8 | 16 | 0.3 | Pumice and Tuff | ||
| VIII | Very loose soft rocks | 0.6 | No blasting needed | |||
| IX | Soil | 0.5 | ||||
| X | Sand | 0.3 | ||||
Shapiro (1988) also used a similar approach though used the term ‘explodability’ to describe the blastability of a rock mass based on powder factor, for underground excavation. The explodability (blastability) was assessed based on defining a reference powder factor (qref (kg/m3) and burden (Bref (cm)), associated with a specific (standard) condition. If the rock mass needs a higher powder factor for fragmentation, then it has a higher blastability. Shapiro (1988) considered a 42 mm drill hole diameter, a hole filling coefficient, fc, of 0.75, an efficiency or utilisation capacity of η = 0.9 for the holes in the cut, and ammonite, 6ZhV, with a density of 850 kg/m3 as the standard (reference) conditions for estimating the blastability of rocks (see Table 2).
Table 2. Classes of rock mass blastability based on powder factor for underground excavation (Shapiro, 1988).
| Blastability class | Values of blastability parameters | Blastability class | Values of blastability parameters | ||
|---|---|---|---|---|---|
| q (kg/m3) | B (cm) | q (kg/m3) | B (cm) | ||
| I | 0.30 to 0.48 | 43.0 to 34.0 | VI | 1.77 to2.23 | 18.0 to 16.0 |
| Av = 0.39 | Av = 38.5 | Av =2.00 | Av =17.0 | ||
| II | 0.48 to 0.71 | 34.0 to 28.0 | VII | 2.23 to 2.72 | 16.0 to 14.0 |
| Av = 0.60 | Av = 31.0 | Av =2.48 | Av =15.0 | ||
| III | 0.71 to 1.00 | 28.0 to 24.0 | VIII | 2.72 to 3.28 | 14.0 to 13.0 |
| Av = 0.86 | Av = 26.0 | Av =3.00 | Av =13.5 | ||
| IV | 1.00 to 1.35 | 24 to 20.0 | IX | 3.28 to 3.92 | 13.0 to 12.0 |
| Av = 1.18 | Av = 22.0 | Av =3.60 | Av =12.5 | ||
| V | 1.35 to 1.77 | 20.0 to 18.0 | X | 3.92 to 4.64 | 12.0 to 11.0 |
| Av = 1.56 | Av = 19.0 | Av =4.28 | Av =11.5 | ||
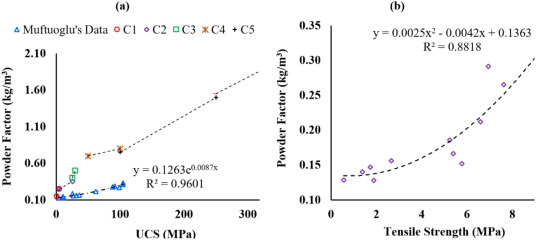
The complexities of defining blastability in terms of a powder factor without understanding the fragmentation outcomes are indicated by the very different suggested powder factors for the same compressive strength between data for surface coal mines in Turkey (Muftuoglu et al., 1991) and the powder factors predicted by Mohamed et al. (2015) (see Fig. 1) and Table 3 (Gokhale, 2010).
 Fig. 1
Fig. 1Table 3. Powder factor estimation based on rock strength, rock density, and joint spacing (Gokhale, 2010).
| Powder factor (kg/m3) | Sj-av (m) | σc (MPa) | ρr (kg/m3) | |
|---|---|---|---|---|
| Range | Average | |||
| 0.12–0.18 | 0.150 | <0.1 | 10–30 | 1400–1800 |
| 0.18–0.27 | 0.225 | 0.10–0.25 | 20–45 | 1750–2350 |
| 0.27–0.38 | 0.320 | 0.20–0.50 | 30–65 | 2250–2550 |
| 0.38–0.52 | 0.450 | 0.45–0.75 | 50–90 | 2500–2800 |
| 0.52–0.68 | 0.600 | 0.70–1.00 | 70–120 | 2750–2900 |
| 0.68–0.88 | 0.780 | 0.95–1.25 | 110–160 | 2850–3000 |
| 0.88–1.10 | 0.990 | 1.20–1.50 | 145–205 | 2950–3200 |
| 1.10–1.37 | 1.235 | 1.45–1.70 | 195–250 | 3150–3400 |
| 1.37–1.68 | 1.525 | 1.65–1.90 | 235–300 | 3350–3600 |
| 1.68–2.03 | 1.855 | >1.85 | >285 | >3550 |
To expand the range of parameters considered in estimating the powder factor, Lilly (1986) proposed a linear relationship between the powder factor needed to fragment iron ore rocks and a blastability index (BI). The blastability index depends on the characteristics of the discontinuities in the rock mass, the strength, and the density of the intact blocks of rocks. The powder factor, q, (kg/m3), can be estimated by:where a1 and b1 are empirical coefficients depending on the diameter of the blast hole and the bench height.
Lilly’s blastability index was initially developed to classify all the rock mass types present in the iron ore mines of the Pilbara area in northwest Western Australia. The index has a maximum value of 100 which reflects the characteristics of the heavily massive and hard, iron-rich cap rocks, in the area with a specific gravity of about 4.0 (tonne/m3). The blastability index could also successfully classify the soft friable shales with indices around 20 or less in the area (Lilly, 1986).
Lilly’s blastability classification is similar to the traditional rock mass classification systems (e.g., RMR and Q-system) which are widely used in tunnelling and underground excavations (Barton, 1988; Bieniawski, 1979). The rock mass information (presented in Table 4) is used to rate the rocks based on their integrity and structures (Lilly, 1986; Lilly, 1992; Widzyk-Capehart and Lilly, 2002). The BI is defined as:where RDI is the Rock Density Index and is related to ρr the rock mass density (ton/m3) by (Lilly, 1986):
Table 4. Rating factors in Lilly's blastability index (Lilly, 1986).
| Parameter | Rating |
|---|---|
| Rock mass description (RMD) | |
| Powdery or friable | 10 |
| Blocky | 20 |
| Massive | 50 |
| Joint plane spacing (JPS) | |
| Close (<0.1 m) | 10 |
| Intermediate (0.1 m to 1.0 m) | 20 |
| Wide (>1.0 m) | 50 |
| Joint plane orientation (JPO) | |
| Horizontal | 10 |
| Dip out of face | 20 |
| Strike normal to face | 30 |
| Dip into face | 40 |
The hardness parameter, Hr, incorporates the effect of strength using (Lilly, 1992):where σc is the uniaxial compressive strength of rocks (MPa).
It is also noteworthy that the BI factors are highly weighted towards the nature and orientation of the widely spaced joint planes. The index attempts to account for the directional effects though the JPO factor, though in highly jointed rock masses it can be challenging to determine which joint set forms the major plane of weakness. A further complication is the large, discrete change in BI for a small change in the parameters of a rock mass. A typical example could be two separate jointed rock masses with identical strength and density. The joint spacing in the first one is 1.0 m while in the second it is 1.1 m. The parameter JPS changes sharply from 20 to 50 which consequently results in a significant difference between the blastability of these two rock masses.
Lilly (1992) also produced a series of design charts (e.g., see Fig. 2 an example of these charts) for estimating the blast patterns (Burden × Spacing) and powder factors for various blasthole diameters. The design charts are for three different bench heights of 5 m, 8 m, and 10 m. The blasthole diameters are also assumed to be 76 mm, 89 mm, 102 mm and 114 mm. It is also assumed that the fragmentation is predictable based on Kuz-Ram model (see Section 2.2.3 and Eq. 9) and %95 of materials shall pass an 800 mm grizzly. It is also assumed that blastholes are vertical, and blasts are drilled in a triangular pattern with (S = 1.16×B), sub-drilling is also assumed to be 8 times the blasthole diameter, and stemming is set to burden size. Anfo was also considered as the charge for the blastholes and it is expected that the initial sequence can provide adequate burden relief and material movement.
 Fig. 2
Fig. 2Similarly, Fig. 3 also shows the application of Bickers et al. (2002) modified BI (see Section 3.3.2 and Fig. 16) to predict the holes standoff and linear charge concentration kg/m in the wall to limit damage from trim blasts in an open-pit iron ore mine in Australia.
 Fig. 3
Fig. 3A proper characterisation of rock mass blastability is needed to use the controllable factor in a way to minimise the undesirable consequences of blasting, such as the ground vibration due to blasting or fly rock (Müller (1997). This means that achieving a good fragmentation and minimising the ground vibration and flyrock are not independent objectives. High ground vibrations can be related to the blastability in terms of the acoustic impedance of the rocks, Ir (kg/m2sec), and this is compounded by the excessive volume of the blast generated gases (see Fig. 13, Fig. 4). Instead of the powder factor, an empirical parameter known as the specific blasting effect, Sg, which is linked to the impulse per unit blast volume (Ns/m3) was proposed, which is defined as (Hohlfeld and Muller, 1999):where Qe is the total mass of the charge (kg), Rv is the ratio of the explosive volume to the borehole volume, Qeh is the heat of the explosion (J/kg), ρe is the density of the explosive (kg/m3), Ab is the surface under stress in the total blast installation (m2). Additionally, Rf denotes the fragmentation ratio, and Ar is the remaining face surface of the total blast installation (m2). Furthermore, Af shows the free surface of the total blast installation (m2), and tb indicates the delay time of the total blast installation (s).
 Fig. 4
Fig. 4The complete description of these parameters can be found in (Hohlfeld and Muller, 1999; Müller, 1997; Müller and Hohlfeld, 1997). The correlations between the specific charge effect, fracture frequency, loosening and fragmentation of rocks, and ground vibration are shown in Fig. 4.
As can be seen in Fig. 4, low levels of loosening and fracturing often occur in smooth blasting which has a small specific blasting effect. By increasing the distribution of charge, the disintegration and fragmentation of the rock mass as well as the specific blasting effects increase. If the specific blasting effects exceed a threshold, which is around 50 Ns/m3, the risks of flyrock increase and must be considered in the blast design. The interrelationships between blast design, site characteristics, and the rock fragmentation, ground vibration, and flyrock could be very complex. Interestingly enough, Müller (1997) mentioned that an increase in the specific blast effect is associated with a decrease in ground vibration. He stated that overcharged blasts with Sg > 50 Ns/m3 yield a smaller vibration effect but impose a much higher risk of flyrock (Müller, 1997).
2.2.3. Fragmentation size prediction
If it is possible to predict the fragmentation caused by a certain set of controllable blast inputs as per Eq. 1, then an inversion will enable the designer to identify the correct design for the desired blast fragmentation size or distribution. Numerous investigations were undertaken by Protodyakonov in the former Soviet Union, over 100 years ago (1909 to 1926), to develop a quantitative approach to analyse the strengths of rocks for different mining applications (Protodyakonov, 1962a, Protodyakonov, 1962b) (See Section 3.1.1). Kutuzov et al. (1974) also reported on some of the old research performed by Protodyakonov for estimating the powder factor based on rock strength/hardness. Since Protodyakonov’s test estimates the amount of fines for a given impact, the approach was also applied by Kuznetsov (1973) to estimate the mean size of the fragmentation generated by the firing of a blasthole. The mean fragment size (cm) is linearly related to the rock factor, AK, and can be estimated as:where AK is the rock mass blastability, Qe is the mass of the explosives (kg), and V is the volume of the rock mass (m3). Fragmentation prediction was developed further in the Kuz-Ram approach by including the particle size distribution, Rx, in the form of an adapted Rosin-Rammler (Rosin and Rammler, 1933) equation (Cunningham, 1983, Cunningham, 2005) so that:where AK-R is the Kuz-Ram rock factor, RWS is the relative weight strength of the explosive with respect to ANFO (in percent). Rx is the mass fraction retained on the screen opening x, xm was defined as the mean fragment size (cm) and n is the uniformity index (ranging between 0.7 and 2). Notably, the Rosin-Rammler uniformity coefficient, n, depends on burden B (m), spacing S (m), bench height H (m), hole diameter (mm), standard deviation of drilling precision W (m), charge length L (m), bottom (BCL) and column (CCL) charge lengths (m) and is independent of the rock mass factor.
Later, a modified version of Lilly’s blastability factor BI (see Eq. 4) was included by Cunningham (1987) to replace the Kuznetsov index AK so the Kuz-Ram rock factor AK-R is 0.12BI. The model has been updated and modified many times (e.g., by Cunningham (2005) and Gheibie et al. (2009)). Reviews of these modifications can be found elsewhere (Ouchterlony and Sanchidrián, 2019; Sanchidrián and Ouchterlony, 2017a). However, for this review, it is important to note that Cunningham (2005) added a blastability calibration factor C(A) that varied between 0.5 and 2.0. A variation between -50 % and +100 % implies that the index does not quantitatively predict the contribution of the rock mass. Additionally, Cunningham (2005) modified the uniformity by a factor to produce a more uniform fragmentation in harder rocks with AK-R > 6. Therefore, the rock factor and the uniformity index in the Kuz-Ram model (see Eq. 9) were amended as:where B, S, H, d, W, L, BCL, and CCL refer to burden (m), spacing (m), bench height (m), hole diameter (mm), the standard deviation of drilling precision (-), charge length (m), bottom charge length (m), and column charge length (m), respectively. An alternative and convenient, blastability index was developed for copper and gold mines and proved to be valid for iron ores in Australia (Scott, 1996, Scott, 2017; Scott et al., 2006) using a multiplicative approach where the blastability is modified by a series of factors. The equivalent Kuz-Ram rock factor, AK-R, can be estimated (Scott and Onederra, 2015a) as:
The strength factor, density factor, and structure factor are shown in Fig. 5 and Eqs (16), (20), (31).
 Fig. 5
Fig. 5Subsequently, a substantial number of similar models have been presented in attempts to accurately predict the fragmentation of rocks after blasting. In particular, Ouchterlony and his teams at the Lulea University of Technology in Sweden and the University of Leoben in Austria; and Sanchidrián and co-workers at the Polytechnic University of Madrid, in Spain, have devoted considerable efforts to developing methods for the reliable estimation of blast-induced particle size distributions. The development of the Swebrec model (also known as the KCO model) (Ouchterlony, 2005; Ouchterlony et al., 2006), the fragmentation-energy fan, FEF, model (Ouchterlony et al., 2017; Segarra et al., 2018), and the distribution-free, DF, (also known as xp-Frag) model (Sanchidrián and Ouchterlony, 2017a, Sanchidrián and Ouchterlony, 2017b) are among the main achievements of these investigations. Further information on the various fragmentation prediction models can also be found in relevant reviews (Ouchterlony and Sanchidrián, 2019; Sanchidrián et al., 2012; Sanchidrián et al., 2014). Here, the scope of this study is not to review all the fragmentation prediction models but to identify the key geological and geotechnical factors controlling the mechanisms of rock fragmentation. The applicability of the existing blastability assessment approaches, for the development of 3D distribution of blastability models for differential blasting input to Grade Engineering, is also investigated.
3. Blastability input factors
There are several different approaches for quantifying the rock mass geological and geotechnical characteristics for the assessment of blastability. It is complex to classify the assessment approaches by their inputs as many use multiple sources and tests, in both the laboratory and field scales. Since the aim of the review is to identify the range and suitability of the different input factors, this section considers how the various features have been helped to assess the blastability of rocks. This includes the laboratory testing of small-scale samples, rock mass measurements, geotechnical ratings, pre-blast indirect measurements, post-blast measurements, and the analysis of multiple blast outcomes.
3.1. Laboratory-scale testing
Many approaches assess the blastability of rocks based solely on the laboratory-scale parameters of rock specimens and they are briefly explained below.
3.1.1. Protodyakonov’s impact hardness/strength index
Protodyakonov and his son (Protodyakonov, 1962a, Protodyakonov, 1962b) developed a blastability assessment known as the rock sturdiness or crushing strength method, which is often referred to as Protodyakonov’s hardness or strength index f (which is shown by fp in this study) (Protodyakonov, 1981). The index is defined as the volume of -0.5 mm fines in a specific container produced by a given number of blows of a known weight and uses units of cm-3. The details of the experimental method can be found in the relevant literature (Brook and Misra, 1970; Protodyakonov, 1962b). Protodyakonov’s strength index has been widely used in rock mechanics and mining applications (Aldorf and Exner, 1986) and has been applied to the assessment of the blastability of rock masses (Protodyakonov, 1981; Zou, 2017).
The values of the blastability parameter AK-R vary, from 7 for rock of medium hardness (fp = 8 to 10), though 10 for hard fissured rock (fp = 10 to 14), and up to 13 for hard and slightly fissured rock (fp = 12 to 16) (Faddeenkov, 1974; Kuznetsov, 1973). Although some efforts were made to explore the applications of Protodyakonov’s method during the 1970s (Brook, 1977; Brook and Misra, 1970), the method was mainly employed in Russia, Eastern Europe, and the countries that used to be a part of the Soviet Union. For example, Baron (1968) tried to relate the size of the crater developed around a blast hole to fp. Additionally, Makhin and Karchevskii (1965) showed that the specific expenditure of explosives, which is defined as the mass (kg) of explosives needed to generate one square meter of the new fracture surface, is directly proportional to the Protodyakonov’s rock strength index. Several revised applications of Protodyakonov’s rock strength index in blast design have also recently been proposed in (Eremenko, 2017; Zairov et al., 2018).
3.1.2. Specific surface energy index
Michik and Dolgov (1966) preferred the specific energy of rock samples after blasting, Es, as being better related to the amount of fracturing energy per unit area of newly formed surfaces. A calorimetric technique was used to determine the surface energy, Es (kg.m), which was defined as (Michik and Dolgov, 1966):where Eb is the whole energy emitted during the blast, Ec is the proportion of the explosive energy passing to the calorimeter in the form of heat. It is also noted that, in these tests, Michik and Dolgov (1966) used spherical charges of PETN weighing 0.70 or 1.20 gr, and the heat emission capacity of the PETN, was recorded to be around 6.276 MJ/kg. The cylindrical rock samples prepared for the tests had 21 cm3 volume and a central hole was embedded in the middle of the samples for the insertion of charges.
The specific surface energy, SEs (kg.m/m2) is then defined as:
The surfaces area of the freshly created fragmented particles, Afr (m2), can simply be estimated as:where Vfr is the volume of the broken rocks (m3) and xm is the mean size of the rock fragments (m) (Michik and Dolgov, 1966).
The specific surface energy, SEs, can be used to approximate the charge, Qe, (in kg) to break up a rock to a specific fragment size. The charge can be computed as (Michik and Dolgov, 1966):where Eh is the heat generated from the firing of a charge (MJ/kg) and fb is a coefficient dependent on the blasting operation conditions as well as the structural features of the rock (blasting efficiency). A few examples of the measured specific energies (Michik and Dolgov, 1966) are shown in Table 5.
Table 5. Specific energy, Es, of different rock types (courtesy of Michik and Dolgov, 1966).